Содержание
Определение и формулы математического маятника
Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.
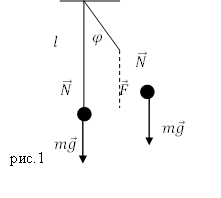
Уравнение движения математического маятника
Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
где $alpha $ — начальная фаза колебаний; $<varphi >_0$ — амплитуда колебаний; $<omega >_0$ — циклическая частота.
Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
Период колебаний математического маятника ($T$) в этом случае равен:
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:
Максимальное значение потенциальной энергии математического маятника равно:
Максимальная величина кинетической энергии:
где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m=<omega >_0x_m$ — максимальная скорость.
Примеры задач с решением
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.
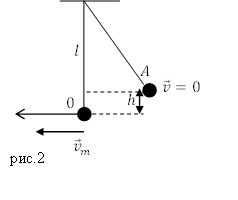
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
Из уравнения (1.1) найдем искомую высоту:
Ответ. $h=frac<2g>$
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми. extit<>
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
Выразим из нее ускорение:
Проведем вычисления ускорения силы тяжести:
Ответ. $g=9,87 frac<м><с^2>$
Основные формулы
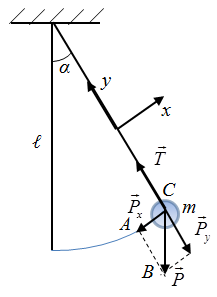
Физическим маятником называется твердое тело, которое может качаться вокруг неподвижной оси. Рассмотрим малые колебания маятника. Положение тела в любой момент времени можно характеризовать углом отклонения его из положения равновесия (рис. 2.1).
Запишем уравнение моментов относительно оси вращения OZ (ось OZ проходит через точку подвеса О перпендикулярно плоскости рисунка "от нас"), пренебрегая моментом сил трения, если известен момент инерции тела
Здесь — момент инерции маятника относительно оси OZ,
— угловая скорость вращения маятника,
Mz=- — момент силы тяжести относительно оси OZ,
a — расстояние от центра тяжести тела С до оси вращения.
Если считать, что при вращении, например, против часовой стрелки угол увеличивается, то момент силы тяжести вызывает уменьшение этого угла и, следовательно, при момент Mz
Сравнивая формулы (3) и (4), заключаем, что период колебаний физического маятника равен периоду колебаний математического маятника с длиной l, называемой приведенной длиной физического маятника:
Период колебаний физического маятника (а, следовательно, и его приведенная длина ) немонотонно зависит от расстояния . Это легко заметить, если в соответствии с теоремой Гюйгенса-Штейнера момент инерции выразить через момент инерции относительно параллельной горизонтальной оси, проходящей через центр масс: Тогда период колебаний будет равен:
Изменение периода колебаний при удалении оси вращения от центра масс O в обе стороны на расстояние а показано на рис. 2.2.
Кинематика колебаний маятника
Маятником является всякое тело, подвешенное так, что его центр тяжести находится ниже точки подвеса. Молоток, висящий на гвозде, весы, груз на веревке — все это колебательные системы, подобные маятнику стенных часов (рис. 2.3).
У всякой системы, способной совершать свободные колебания, имеется устойчивое положение равновесия. У маятника — это то положение, при котором центр тяжести находится на вертикали под точкой подвеса. Если мы выведем маятник из этого положения или толкнем его, то он начнет колебаться, отклоняясь то в одну, то в другую сторону от положения равновесия. Наибольшее отклонение от положения равновесия, до которого доходит маятник, называется амплитудой колебаний. Амплитуда определяется тем первоначальным отклонением или толчком, которым маятник был приведен в движение. Это свойство — зависимость амплитуды от условий в начале движения — характерно не только для свободных колебаний маятника, но и вообще для свободных колебаний очень многих колебательных систем.
Если прикрепить к маятнику волосок — кусочек тонкой проволочки или упругой нейлоновой нити — и будем двигать под этим волоском закопченную стеклянную пластинку, как показано на рис. 2.3. Если двигать пластинку с постоянной скоростью в направлении, перпендикулярном к плоскости колебаний, то волосок прочертит на пластинке волнистую линию (рис. 2.4). Мы имеем в этом опыте простейший осциллограф — так называются приборы для записи колебаний. Кривые, которые записывает осциллограф, называются осциллограммами. Таким образом, рис. 2.2.3. представляет собой осциллограмму колебаний маятника. Амплитуда колебаний изображается на этой осциллограмме отрезком АВ, дающим наибольшее отклонение волнистой кривой от прямой линии ab, которую волосок прочертил бы на пластинке при неподвижном маятнике (покоящемся в положении равновесия). Период изображается отрезком CD, равным расстоянию, на которое передвигается пластинка за период маятника.
Запись колебаний маятника на закопченной пластинке
Осциллограмма колебаний маятника: АВ — амплитуда, CD — период
Так как мы двигаем закопченную пластинку равномерно, то всякое ее перемещение пропорционально времени, в течение которого оно совершалось. Мы можем сказать поэтому, что вдоль прямой аb в определенном масштабе (зависящем от скорости движения пластинки) отложено время. С другой стороны, в направлении, перпендикулярном к аb, волосок отмечает на пластинке расстояния конца маятника от его положения равновесия, т.е. путь, пройденный концом маятника от этого положения. Таким образом, осциллограмма есть не что иное, как график движения — график зависимости пути от времени.
Как мы знаем, наклон линии на таком графике изображает скорость движения. Через положение равновесия маятник проходит с наибольшей скоростью. Соответственно этому и наклон волнистой линии на рис. 2.2.3. наибольший в тех точках, где она пересекает прямую ab. Наоборот, в моменты наибольших отклонений скорость маятника равна нулю. Соответственно этому и волнистая линия на рис. 4 в тех точках, где она наиболее удалена от ab, имеет касательную, параллельную ab, т. е. наклон, равный нулю.
Математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити, и совершавшая колебания в вертикальной плоскости под действием силы тяжести. Если отклонить маятник от положения равновесия, то сила тяжести и сила упругости будут направлены под углом. Равнодействующая сила уже не будет равна нулю. Под воздействием этой силы маятник устремится к положению равновесия, но по инерции движение продолжится и маятник отклоняется в другую сторону. Равнодействующая сила его снова возвращает.
Частота математического маятника — Чем больше период колебаний математического маятника, тем меньше частота.
Важно где происходят колебания! На Луне и на Земле один и тот же математический маятник при одинаковых начальных условиях колебаться будет по-разному. Так как ускорение свободного падения на Луне отличается от ускорения свободного падения на Земле.
Линейная скорость материальной точки, линейное ускорение материальной точки, единицы измерения. Сложение скоростей.
линейная скорость — это производная от пройденного пути по времени.
Отдельные точки вращающегося тела имеют различные линейные скорости 
(метр/сек). Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости 
определяется скоростью вращения тела 
и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени 
тело повернулось на угол 
Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный :
Линейная скорость точки по определению:
линейное ускорение — это производная от скорости по времени.
Формула линейного ускорения:
a = dv/dt = d 2 s/dt 2 , где s – путь,пройденный телом.
Сложение скоростей — с помощью данного закона определяется скорость движения тела относительно неподвижной системы отсчёта. Она равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы
Для того, чтоб было более понятно, как работает закон сложения скоростей, рассмотрим такой пример. Вагон движется со скоростью 50 кмч (это будет 
), в вагоне идет человек со скоростью 3 кмч (это будет 
), найти скорость человека относительно Земли.
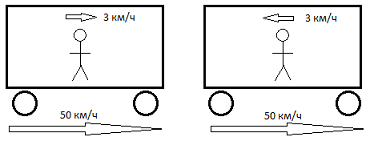У данной задачи будет два решения. Если человек будет идти по направлению движения вагона, то скорость человека относительно Земли будет 53 кмч.
А если человек будет идти против движения вагона, то скорость человека относительно Земли будет 47 кмч.
В Формуле мы использовали :
— Конечная скорость тела
— Скорость тел в различных инерциальных системах отчета
Свободные колебания. Пружинный маятник. Частота колебаний пружинного маятника (формула).
Колебания называются свободными (или собственными), если они совершаются за счет первоначальной сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания).
Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины.
Частота пружинного маятника — Чем больше период колебаний пружинного маятника, тем меньше частота
— Частота Пружинного маятника, 
— Период колебаний маятника
— Масса груза, или масса маятника, 
— Жесткость пружины
Угловая скорость, частота вращения, период вращения (определение, единицы измерения, связь между величинами). Связь между линейной и угловой скоростями.
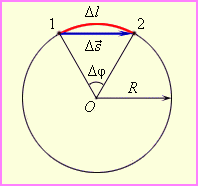
Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость точки. Направление вектора линейной скорости всегда совпадает с касательной к окружности
Точка, лежащая на окружности радиусом R, за один оборот пройдет путь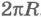 
. Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так:
Так как 
, то
Условия возникновения затухающих колебаний (соотношение между собственной частотой и коэффициентом затухания). Амплитуда затухающих колебаний (формула).
Соотношение: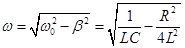 
β — коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.
Амплитуда колебаний — это максимальное расстояние, на которое удаляется колеблющееся тело от своего положения равновесия. Амплитуда затухающих колебаний изменяется по закону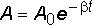 
, где А0 – начальная амплитуда. Зависимость амплитуды показана на рис. 8.3.
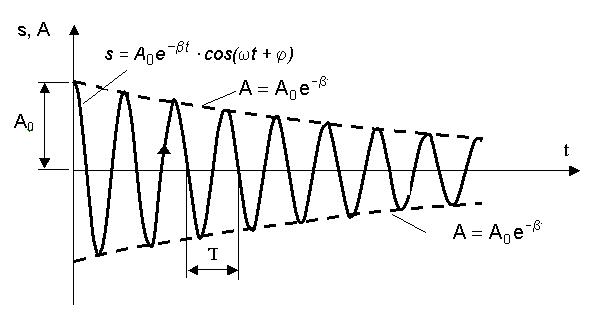Рис. 8.3. График затухающих колебаний
Механическая работа (определение, единицы измерения). Мощность силы (определение, единицы измерения).
Механическая рабоат — то скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы и равна произведению модуля силы F на модуль перемещения S и на косинус угла 
между ними
Если тело под действием силы 
совершает перемещение 
, работа А этой силы равна скалярному произведению силы на вектор перемещения. Работа силы есть скалярная величинаА=
А=
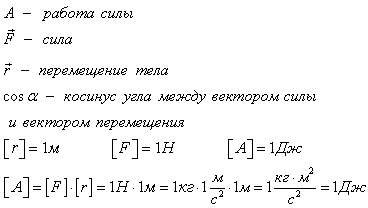
мощность силы — скалярная физическая величина N, равная отношению работы А, совершаемой силой, к промежутку времени 
, в течение которого она совершается:
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа: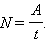 
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с. 
Если тело движется прямолинейно и на него действует постоянная сила, то она совершает работу 
. Поэтому мощность этой силы
