Логические операции с примерами

Содержание

Основные логические операции

Существует три основных логических операции при помощи которых можно записать любое логическое выражение (не пугайтесь):

1. Инверсия
2. Конъюнкция
3. Дизъюнкция

Конъюнкция , оно же «Логическое И», оно же «Логическое умножение».
Мы выбираем название «Логическое И» – оно чаще встречается в программировании.
Допустим, у нас есть два простых выражения – А и В. Эти выражения могут иметь значения или 1 (истина), или 0 (ложь). При выполнении операции «Логическое И» мы получим сложное выражение которое примет значение 1 (истина) только в том случае если и А, и В имеют значение 1 (истина), во всех других случаях результат будет 0 (ложь).
Операция «Логическое И» имеет обозначения (в языках программирования): И, &&, AND, &.

Дизъюнкция , оно же «Логическое ИЛИ», оно же «Логическое сложение».
Мы выбираем название «Логическое ИЛИ». Кстати, если логически подумать, то можно и догадаться какие результаты будут при выполнении этой операции.
В «Логическом И» результат равен 1, если и А, и В, равны 1, а в «Логическом ИЛИ» результат будет равен 1, если или А, или В, равны единице.
Операция «Логическое ИЛИ» имеет обозначения: ИЛИ, ||, OR, | .

Инверсия , оно же «Логическое НЕ», оно же «Отрицание».
Мы выбираем название «Логическое НЕ».
Операция «Логическое НЕ» имеет обозначения: НЕ, !, NOT .
Тут вообще все просто:
Если А=1 (истина), то после выполнения операции «Отрицание» А примет значение 0, то есть становится ложным. И наоборот.
Есть еще одно название этой операции «Инвертор», а применяется оно в отношении цифровых микросхем.

В программировании часто применяется еще одна логическая операция – симбиоз «Логического И» и «Логического ИЛИ»:
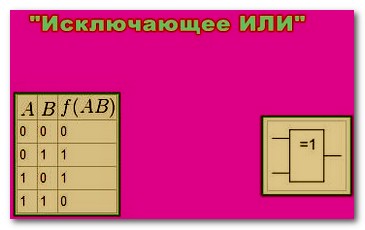
Строгая дизъюнкция , оно же «Исключающее ИЛИ», оно же «Логическое сложение, исключающее ИЛИ», оно же «Сложение по модулю 2»
Мы выбираем название «Исключающее ИЛИ»
Операция «Исключающее ИЛИ» имеет обозначения: Искл.ИЛИ, XOR, ^ .
В этом случае, при выполнении операции «Исключающее ИЛИ», результат будет истинен (равен 1), если А не равно В. В остальных случаях результат будет равен 0 (ложный).

Таблица истинности

Все логические выражения, получающиеся из логических операций, можно свести в таблицы, которые называются таблицы истинности

Таблицы истинности

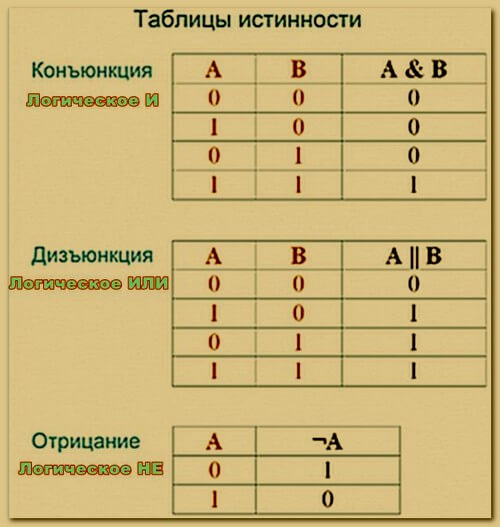
Логические элементы

Логические операции – основа цифровой техники. Даже цифровые микросхемы, которые предназначены только для выполнения логических операций, называют – «логические микросхемы» , или еще проще – «логика» .
Немного остановимся на микросхемах логики и мы.
Работа цифровых микросхем логики основана на выполнение трех основных логических операций, с которыми мы ознакомились выше. Сочетание этих логических операций позволило создать большое количество цифровых микросхем логики.
Основа таких микросхем – логический элемент.

Логический элемент выполняющий операцию «Логическое И»

Логический элемент выполняющий операцию «Логическое ИЛИ»

Логический элемент выполняющий операцию «Логическое НЕ»

Логический элемент выполняющий операцию «Исключающее ИЛИ»

Логический элемент выполняющий операцию «Логическое ИЛИ-НЕ»

Логический элемент выполняющий операцию «Логическое И-НЕ»

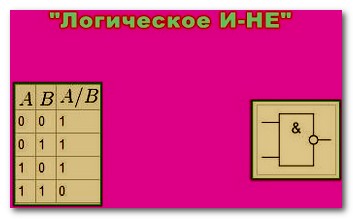
Кроме таких комбинаций логических операций существует еще ряд других.

Кстати, есть еще одна разновидность логики – женская логика. Весьма интересная штука. Но так как она к сегодняшней теме не относится, то придется, к сожалению, этот вопрос опустить.

(25 голосов, оценка: 4,68 из 5)

Презентация к уроку

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели:

оказание помощи учащимся при решении задач, где необходимо построение таблиц истинности, применение логических операций в простых и сложных выражениях;
оказание помощи учащимся при подготовке к ЕГЭ;
оказание помощи учителю при организации подготовки учащихся к ЕГЭ.

Задачи:

отработать навыки по формированию представления об истории возникновения и эволюции логического мышления;
отработать навыки составления однозначной интерпретации произвольной информации на основе алгебры логики;
совершенствовать навыки формирования информационной культуры и потребности в приобретении знаний;
совершенствовать навыки самостоятельной работы.

Тип урока: Данный урок подходит как для изучения нового материала, так и для закрепления изученного.

Ход урока:

1. Организационный момент. Приветствие учащихся.

2. Теоретический материал: изучение, повторение

Историческая справка. Логика – это очень древняя наука.

Основы формальной логики заложил ученый Древней Греции – Аристотель (384 г.-322 г. до н.э.) . Заслуга ученого состоит в том, что он отделил форму мышления от содержания, попытался соединить логику и математику, разработал раздел теории доказательств.

Немецкий ученый Лейбниц (1646-1716) взглянул на логику Аристотеля через призму математики. Им написан трактат — “Азбука мыслей”, сжатый и краткий язык символов. Лейбниц разработал идею логического исчисления. Рассуждения обозначил буквами, сложные высказывания — формулами. В результате удалось содержательные рассуждения заменить формальными вычислениями.

Джордж Буль считается основоположником математической логики как самостоятельной дисциплины. В его работах логика обрела свой алфавит, свою орфографию и грамматику. Буль — автор известных произведений, в т.ч. работы “Математический анализ логики”(1847г.). Основной труд Джорджа Буля — “Исследование законов мысли”, в котором представлен раздел логики — алгебра высказываний.

Логика — это наука о формах и способах мышления.

Основными формами мышления являются

понятие,
высказывание,
умозаключение.

Понятие — это форма мышления, фиксирующая основные, существенные признаки объекта.

Пример. Клавиатура — устройство ввода символьной информации в компьютер.

Высказывание (суждение) — это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо ложным, либо истинным.

Пример: Все дети любят лечить зубы (ложь).

Все взрослые были детьми (истина).

Умозаключение — это форма мышления, с помощью которой из одного или нескольких суждений, может быть получено новое суждение (заключение).

Пример: доказательство теорем в геометрии.

Алгебра высказываний

Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание.

В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: “истина” (1) и “ложь” (0).

Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок “и”, “или”, “не”.

Логическое отрицание (инверсия)

Присоединение частицы “не” к высказыванию называется операцией логического отрицания или инверсией.

На естественном языке: неверно, что. не

А – “Сегодня идет снег”

¬ А – “Неверно, что сегодня идет снег” или “Сегодня не идет снег”

Таблица истинности логического отрицания

А ¬ А

0 1

1 0

Инверсия высказывания истинна, если высказывание ложно, и ложна, когда высказывание истинно.

Логическое умножение (конъюнкция)

Объединение двух (или нескольких) высказываний в одно с помощью союза “и” называется операцией логического умножения или конъюнкцией.

На естественном языке: И.

Пример. А ^ B – “Сегодня светит солнце И дождь”

Таблица истинности логического умножения

А В А ^ B

0 0 0

0 1 0

1 0 0

1 1 1

Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно из высказываний ложно.

Логическое сложение (дизъюнкция)

Объединение двух (или нескольких) высказываний с помощью союза “или” называется операцией логического сложения или дизъюнкцией.

На естественном языке: ИЛИ.

Пример. А V B – В вазе лежат “яблоки” ИЛИ “груши”

Таблица истинности логического сложения

А В А V B

0 0 0

0 1 1

1 0 1

1 1 1

Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно из высказываний истинно.

Логическое следование (импликация)

На естественном языке: если. то.

Пример. А —> B – Если выучить материал, то сдашь зачет.

Таблица истинности логического следования

А В А —> B

0 0 1

0 1 1

1 0 0

1 1 1

Импликация двух высказываний ложна только тогда, когда из истины следует ложь, и истинна в остальных случаях.

Логическое равенство (эквивалентность)

Обозначение: , , =.

На естественном языке: тогда и только тогда, когда

Пример. А B – Добиться результата в спорте можно тогда и только тогда, когда приложено максимум усилий.

Таблица истинности логического равенства

А В А B

0 0 1

0 1 0

1 0 0

1 1 1

Эквивалентность двух высказываний истина только тогда, когда оба высказывания одновременно либо ложны, либо истинны.

Порядок выполнения логических операций в сложном логическом выражении:

Инверсия ¬;
Конъюнкция ^;
Дизъюнкция V;
Импликация >;
Эквивалентность .

Для изменения указанного порядка выполнения логических операций используются скобки.

3. Практическая работа.

Учащиеся выполняют задания. (презентация, слайды 17-23). После выполнения задания учащиеся проверяют правильность решения.

Задание 1: Заполните таблицу. Истина – 1, Ложь — 0

Высказывание	параллелограмм	прямоугольник	ромб	квадрат
Противолежащие стороны параллельны и равны.
Все стороны равны.
Противолежащие углы равны, сумма соседних углов равна 180° .
Все углы прямые.
Диагонали пересекаются и точкой пересечения делятся пополам.
Диагонали равны.
Диагонали взаимно перпендикулярны и являются биссектрисами его углов.

Задание 2: Запишите высказывание “если яблоко зеленое или мелкое, то оно твердое”, используя знаки логических операций.

Задание 3: Определите результат логического выражения при заданных параметрах

Задание 4: Для какого имени истинно высказывание:

(Первая буква гласная) / (Четвёртая буква согласная) / (B слове четыре буквы)?

1) СЕРГЕЙ
2) АЛЕКСЕЙ
3) АНТОН
4) ИЛЬЯ

Задание 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:

Y	F
0	0
1	0
0	0

Какое выражение соответствует F?

1) (X ^ Y) ? (X Z)
2) (X ^ Y) ? (X Z)
3) (¬Х ^ Y) ? (X Z)
4) ¬(X ^ Y) ? (X Z)

4. Итоги урока. Вопросы учеников.

5. Домашнее задание. Учить конспект, придумать аналогичные задания.

6. Подведение итогов урока

Анализ и оценка успешности достижения цели занятия. Определение перспективы последующей работы.

Методы вычисления

Логика выражений необходима для строения составных высказываний. Они состоят из простых выражений за счет соединения их друг с другом при помощи операций логики «не», «и», «или». Для определения ложности либо истинности рассматриваются составные символы.

При передачи данных через онлайн-сервисы и с помощью ЭВМ операторы используют специализированные термины. Под высказываниями подразумеваются повествовательные предложения, которые могут быть истинными (1) либо ложными (0). Операция — мыслительное действие, в результате которого изменяется объём либо содержание, образуется новое понятие.

Элементы выражения, утверждения либо записи:

С учётом значений переменных выражение может иметь одно из следующих значений: истина либо ложь. Составные выражения строятся из простых при помощи логических действий, которые соответствуют связкам, употребляемым в естественном языке. Пример: значение инверсии — «неверно, что», а конъюнкции — «и», «но», «хотя». Существует определённый порядок выполнения логических операций в информатике:

отрицание (инверсия);
умножение (конъюнкция);
сложное и простое сложение (дизъюнкция);
следствие (импликация);
тождество (эквивалентность).

Для изменения последовательности, указанной в схеме, применяются скобки. К сложным функциям относится конъюнкция.

Согласно формуле, истинно в том и только в том случае, если 2 простых высказывания являются истинными. Подобное значение возможно в одном случае, а во всех других оно ложное. Обозначение конъюнкции: &, ∧.

Описание операций:

= «основателем высшей математики является Буль»;
= «графические исследования Шеннона используются в алгебре».

Выражение считается истинным, когда одновременно истинны два высказывания. Базовые значения исходных данных указываются в специальной таблице истинности логических операций. Двоичные числа, которые соответствуют высказываниям, располагаются в схеме в возрастающем порядке. В последнем столбике записывается результат выполненных операций для конкретных операндов (аргумент). Свойства логического умножения:

если один элемент ложный, тогда вся конъюнкция ложная для конкретного набора значений;
если выражения истинны, тогда всё уравнение будет истинной;
результат всей конъюнкции сложного высказывания не зависит от порядка следования элементов.

Логическое сложение

В информатике часто используется такой вид операции, как дизъюнкция. Случай, когда нужно исключать истинное сложение — все подвыражения ложны. Символы, которые используются для обозначения операции: +, ∨. Базис свойств сложного сложения:

любое подвыражение истинно, значит, вся дизъюнкция будет истинной;
если все определения из списка ложны, тогда вся дизъюнкция ложна.

Результат не зависит от порядка расположения знаков логической операции. Для решения дизъюнкции используются 2 выражения. Первое: = «Лейбниц применил в информатике математические символы», второе: = «Лейбниц основал бинарную арифметику».

В результате преобразования описанных выражений получается следующий результат: «Идея использования в информатике математических символов принадлежит Лейбницу, или он основал бинарную арифметику».

Сложное высказывание считается ложным, если одновременно неверны два первоначальных понятия. В основе записи дизъюнкции находятся нули и единицы.

Использование частиц

Инверсия — ещё одна операция, которую применяют ежедневно операторы ЭВМ для обработки и передачи данных. Принцип преобразования отрицания: каждому тезису ставится новое высказывание, противоположное первоначальному. Инверсия либо отрицание означает, что к исходному выражению приставляется частица «не» либо слово «неверно», «что». Расшифровка логической операции:

если первоначальное выражение является истиной, тогда его отрицание будет ложным;
если исходное высказывание ложное, тогда его отрицание будет истинным.

Чтобы править запись инверсии, применяются специальные знаки логической операции: «НЕ», «А», «¬А». Для логического отрицания характерны некоторые свойства. Считается, что «двойное отрицание» (обозначается «¬ ¬A») — следствие суждения А. Оно указывает на тавтологию логического формата и равняется значению в булевой логистике.

Высказывание «Я имею компьютер» имеет отрицание «Неверно, что я имею компьютер» либо «У меня нет компьютера». Выражение «Я не знаю японский язык» имеет отрицание «Неверно, что я не знаю японский язык» либо «Я знаю японский язык». Другой пример инверсии: «Все ученицы 8 класса — отличницы». Отрицание можно составить следующим образом:

«неверно, что все ученицы 8 класса — отличницы»;
«не все ученицы 8 класса — отличницы».

Когда строится отрицание к простому высказыванию, либо применяется оборот из русского языка «неверно, что…», либо отрицание формируется для сказуемого, тогда к глаголу рекомендуется добавить частицу «не». Логическое умножение с символом «и» должно выполняться раньше сложения с «или».

Сложную операцию можно записать в виде выражения, в состав которого входят переменные, знаки и скобки. При этом необходимо соблюдать некоторую последовательность действий:

Для изменения порядка выполнения действия расставляются скобки. В конце выполненных операций проводится импликация. Это сложное выражение считается истинным в любом случае, исключение — из истины следует ложь. Операция позволяет связать 2 простых высказывания, из которых первое считается условием, а второе — следствием.

Для вычисления результата составного высказывания достаточно выяснить только значение 1 составного элемента. Если в схеме с «и» используется ложное простое высказывание, то результат составного будет ложным. Когда в составном предложении с «или» значения одного простого символа истинное, тогда результат всего выражения будет истинным.

Закон Пирса

В информатике используется булевая функция, названная в честь Пирса. Впервые стрелку Пирса ввели ученые в алгебру в 1880 г. г. Она обозначается следующим образом: ↓, «или-не». Свойства функции:

формирование базиса для булевых функций 2-х неизвестных;
построение других операций (отрицание: X↓X=¬X).

В информатике выражение представлено в виде элемента, который называется «операция 2ИЛИ-НЕ». Другая функция, которая часто применяется в электронике, называется штрихом Шеффера. Операция состоит из 2-х неизвестных либо бинарного элемента. Штрих используется с 1913 года. Он обозначается как |, что эквивалентно «и-не».

Его главные свойства:

основа функции, состоящей из 2-х переменных;
возможность построения иных высказываний (X ∣ X=¬X — отрицание).

В информатике операция используется с целью реализации схем путём применения типового, но дорогостоящего элемента. Из всех существующих логических операций приоритет отдаётся инверсии. Чтобы выразить логические сущности, операторы применяют разные символы. Специалисты решают задачи в уме, передавая через сервисы только конечный результат. Для обработки данных они используют схемы всех высказываний. Вычисления производятся быстрее на ЭВМ, компьютерах с мощным жёстким диском.