Ветвь и узел электрической цепи
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. В зависимости от особенностей схемы следует применять тот или иной способ расчета электрической цепи. В данном разделе рассмотрим ключевые понятия, которые в дальнейшем будут необходимы для выбора наиболее оптимального и правильного приема решения задач.
Ветвью называется участок электрической цепи, обтекаемый одним и тем же током. Ветвь образуется одним или несколькими последовательно соединенными элементами цепи.
Узел — место соединения трех и более ветвей.
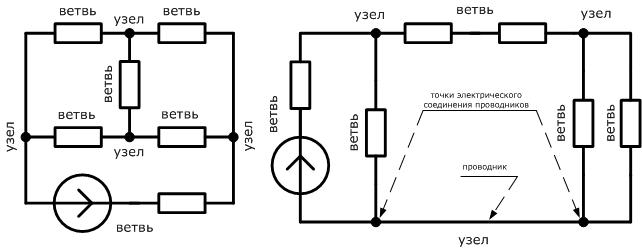
В качестве примера на рисунке изображены схемы двух электрических цепей. Первая из них содержит 6 ветвей и 4 узла. Вторая состоит из 5 ветвей и 3 узлов. В этой схеме обратите внимание на нижний узел. Очень часто допускают ошибку, считая что там 2 узла электрической цепи, мотивируя это наличием на схеме цепи в нижней части 2-х точек соединения проводников. Однако на практике следует считать две и более точки, соединенных между собой проводником, как один узел электрической цепи.
При обходе по соединенным в ветвях цепям можно получить замкнутый контурэлектрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел встречается в данном контуре не более одного раза. Ниже приведена электрическая схема, на которой отмечено несколько произвольно выбранных контуров.
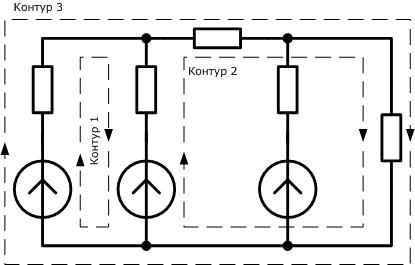Всего для данной цепи можно выделить 6 замкнутых контуров.
Закон Ома
Данный закон очень удобно применять для ветви электрической цепи. Позволяет определить ток ветви при известном напряжении между узлами, к которым данная ветвь подключена. Также позволяет буквально в одно действие рассчитать одноконтурную электрическую цепь.
При применении закона Ома предварительно следует выбрать направление тока в ветви. Выбор направления можно осуществить произвольно. Если при расчете будет получено отрицательное значение, то это значит, что реальное направление тока противоположно выбранному.
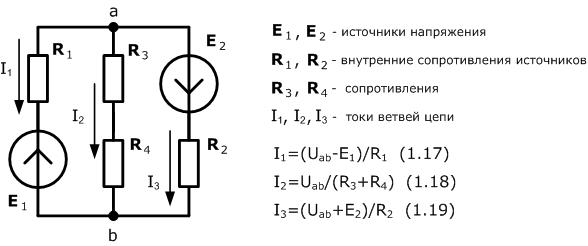
Для ветви, состоящей только из резисторов и подключенной к узлам электрической цепиa и b (см. рис.) закон Ома имеет вид:
Соотношение (1.15) написано в предположении, что выбрано направление тока в ветви от узла a к узлу b. Если мы выберем обратное направление, то числитель будет иметь вид: (Ub-Ua). Теперь становится понятно, что если в соотношении (1.15) возникнет ситуация, когда Ub>Ua то получим отрицательное значение тока ветви. Как уже упоминалось выше, это значит, что реальное направление тока противоположно выбранному. Примером практического применения данного частного случая закона Ома при расчетах электрических цепей является соотношение (1.18) для электрической цепи, изображенной на рисунке.
Для ветви содержащей резисторы и источники электрической энергии закон Ома принимает следующий вид:
Соотношение (1.16) написано в предположении, что предварительно выбрано напавление тока от узла a к узлу b. При расчете алгебраической суммы ЭДС ветви следует знак "+" присваивать тем ЭДС, чье направление совпадает с направлением выбранного тока ветви (направление ЭДС определяется направлением стрелки в обозначении источника электрической энергии). Если направления не совпадают, то ЭДС берется со знаком "-". На рисунке есть примеры применения данного варианта закона Ома — соотношения (1.17) и (1.19)
Если необходимо рассчитать одноконтурную электрическую цепь с произвольным количеством источников электрической энергии и резисторов, то следует применять соотношение (1.16), имея ввиду что Ua=Ub.
Линейные и нелинейные электрические цепи
Линейной электрической цепью называют такую цепь, все компоненты которой линейны. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы(подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и катушки индуктивности. Если цепь содержит отличные от перечисленных компоненты, то она называется нелинейной.
Изображение электрической цепи с помощью условных обозначений называют электрической схемой. Функция зависимости тока, протекающего по двухполюсному компоненту, от напряжения на этом компоненте называется вольт-амперной характеристикой (ВАХ). Часто ВАХ изображают графически в декартовых координатах. При этом по оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток.
В частности, омические резисторы, ВАХ которых описывается линейной функцией и на графике ВАХ являются прямыми линиями, называют линейными.
Примерами линейных (как правило, в очень хорошем приближении) цепей являются цепи, содержащие толькорезисторы, конденсаторы и катушки индуктивности без ферромагнитных сердечников.
Некоторые нелинейные цепи можно приближенно описывать как линейные, если изменение приращений токов или напряжений на компоненте мало, при этом нелинейная ВАХ такого компонента заменяется линейной (касательной к ВАХ в рабочей точке). Этот подход называют «линеаризацией». При этом к цепи может быть применён мощный математический аппарат анализа линейных цепей. Примерами таких нелинейных цепей, анализируемых как линейные относятся практически любые электронные устройства, работающие в линейном режиме и содержащие нелинейные активные и пассивные компоненты (усилители, генераторы и др.).
электрическая цепь – это отдельно взятая группа электроприборов (утюги, блоки телевизоры, холодильники и т. д.) совместно с розетками, выключателями, проводами, автоматами и электрической подстанцией (как же без нее получить ток) на данный момент работающих совместно для достижения определенной цели. Ну а вот в зависимости от цели (просмотра любимой передачи, сохранения свежести продуктов или обеспечения стабильности питающих параметров в блоке питания компьютера) электрические цепи подразделяются на простые и сложные, неразветвленные и разветвленные, линейные и нелинейные.
То есть электрическую цепь можно рассматривать как совокупность отдельных электрических устройств, так и совокупность дискретных простейших деталей и связей между ними образующих один из функциональных блоков в электрической схеме какого-то устройства.
Неразветвленныеэлектрические цепи – они же простые – это цепи в которых ток течет не меняя свое значение и по простейшему пути от источника энергии до потребителя. То есть через все элементы этой цепи течет один и тот же ток. Простейшей неразветвленной цепью можно считать цепь освещения одной из комнат в квартире, где используется однорожковая люстра. В данном случае ток течет от источника энергии через автомат, выключатель, лампочку и обратно к источнику энергии.
Разветвленные– это цепи имеющие одно или более ответвленных путей протекания тока. То есть ток начиная свой путь от источника энергии разветвляется на несколько ветвей потребителей, при этом меняя свое значение. Одним из несложных примеров такой цепи является приведенная выше цепь освещения комнаты в квартире, но только с многорожковой люстрой и многоклавишным выключателем. Ток от источника энергии доходит через автомат к многоклавишному выключателю, а дальше разветвляется на несколько ламп люстры, а далее через общий провод обратно к источнику энергии.
Линейной считается такая электрическая цепь, где характеристики всех ее элементов не зависят от величины и характера протекающего тока и приложенного напряжения.
Нелинейной считается цепь содержащая хотя бы один элемент, характеристики которого зависят от протекающего тока и приложенного напряжения.
2. Эквивалентные преобразования в электрических цепях. Определение эквивалентного сопротивления при последовательном, параллельном и смешанном соединении элементов электрических цепей.
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.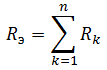 
Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
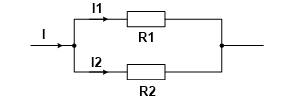
При параллельном соединении эквивалентное сопротивление находится как: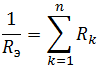 
В случае двух параллельно соединенных резисторов
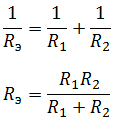
В случае трех параллельно подключенных резисторов:
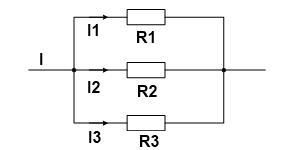
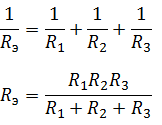
Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
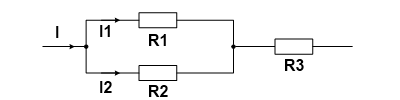
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R3. Следует понимать, что после преобразования эквивалентное сопротивление R1R2 и резистор R3, соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема соединения представлена на рисунке ниже.
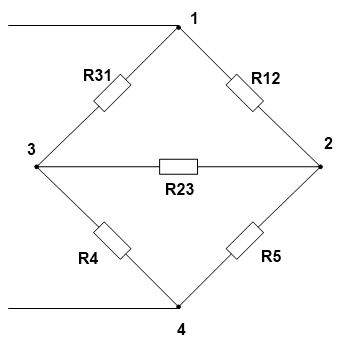
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
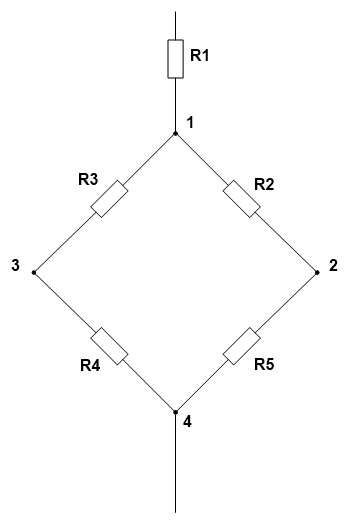
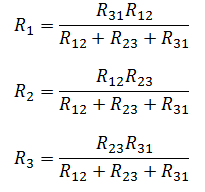
Затем находят общее эквивалентное сопротивление, учитывая, что резисторы R3,R4 и R5,R2 соединены между друг другом последовательно, а в парах параллельно.
Те элементы электрической цепи, для которых зависимость тока от напряжения I(U) или напряжения от тока U(I), а также сопротивление R, постоянны, называются линейными элементами электрической цепи. Соответственно и цепь, состоящая из таких элементов, именуется линейной электрической цепью.
Для линейных элементов характерна линейная симметричная вольт-амперная характеристика (ВАХ), выглядящая как прямая линия, проходящая через начало координат под определенным углом к координатным осям. Это свидетельствует о том, что для линейных элементов и для линейных электрических цепей закон Ома строго выполняется.
Кроме того речь может идти не только об элементах, обладающих чисто активными сопротивлениями R, но и о линейных индуктивностях L и емкостях C, где постоянными будут зависимость магнитного потока от тока — Ф(I) и зависимость заряда конденсатора от напряжения между его обкладками — q(U).
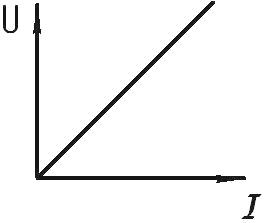
Яркий пример линейного элемента — проволочный резистор. Ток через такой резистор в определенном диапазоне рабочих напряжений линейно зависит от величины сопротивления и от приложенного к резистору напряжения.
Если же для элемента электрической цепи зависимость тока от напряжения или напряжения от тока, а также сопротивление R, непостоянны, то есть изменяются в зависимости от тока или от приложенного напряжения, то такие элементы называются нелинейными, и соответственно электрическая цепь, содержащая минимум один нелинейный элемент, окажется нелинейной электрической цепью.
Вольт-амперная характеристика нелинейного элемента уже не является прямой линией на графике, она непрямолинейна и часто несимметрична, как например у полупроводникового диода. Для нелинейных элементов электрической цепи закон Ома не выполняется.
В данном контексте речь может идти не только о лампе накаливания или о полупроводниковом приборе, но и о нелинейных индуктивностях и емкостях, у которых магнитный поток Ф и заряд q нелинейно связаны с током катушки или с напряжением между обкладками конденсатора. Поэтому для них вебер-амперные характеристики и кулон-вольтные характеристики будут нелинейными, они задаются таблицами, графиками или аналитическими функциями.
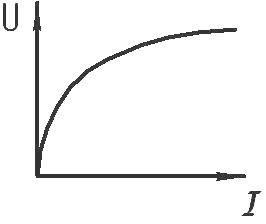
Пример нелинейного элемента — лампа накаливания. С ростом тока через нить накаливания лампы, ее температура увеличивается и сопротивление возрастает, а значит оно непостоянно, и следовательно данный элемент электрической цепи нелинеен.
Для нелинейных элементов свойственно определенное статическое сопротивление в каждой точке их ВАХ, то есть каждому отношению напряжения к току, в каждой точке на графике, — ставится в соответствие определенное значение сопротивления. Оно может быть посчитано как тангенс угла альфа наклона графика к горизонтальной оси I, как если бы эта точка лежала на линейном графике.
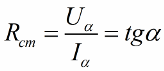
Еще у нелинейных элементов есть так называемое дифференциальное сопротивление, которое выражается как отношение бесконечно малого приращения напряжения — к соответствующему изменению тока. Данное сопротивление можно посчитать как тангенс угла между касательной к ВАХ в данной точке и горизонтальной осью.
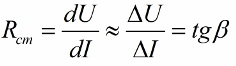
Такой подход делает возможным простейший анализ и расчет простых нелинейных цепей.
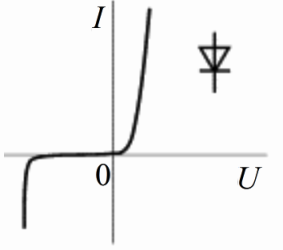
На рисунке выше показана ВАХ типичного диода. Она располагается в первом и в третьем квадрантах координатной плоскости, это говорит нам о том, что при положительном или отрицательном приложенном к p-n-переходу диода напряжении (в том или ином направлении) будет иметь место прямое либо обратное смещение p-n-перехода диода. С ростом напряжения на диоде в любом из направлений ток сначала слабо увеличивается, а после резко возрастает. По этой причине диод относится к неуправляемым нелинейным двухполюсникам.
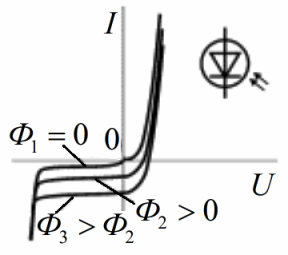
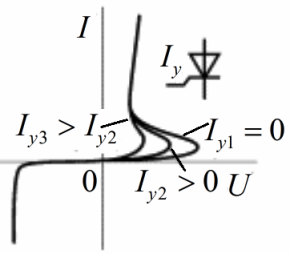
На этом рисунке показано семейство типичных ВАХ фотодиода в разных условиях освещенности. Основной режимом работы фотодиода — режим обратного смещения, когда при постоянном световом потоке Ф ток практически неизменен в довольно широком диапазоне рабочих напряжений. В данных условиях модуляция освещающего фотодиод светового потока, приведет к одновременной модуляции тока через фотодиод. Таким образом, фотодиод — это управляемый нелинейный двухполюсник.
Это ВАХ тиристора, здесь видна ее явная зависимость от величины тока управляющего электрода. В первом квадранте — рабочий участок тиристора. В третьем квадранте начало ВАХ — малый ток и большое приложенное напряжение (в запертом состоянии сопротивление тиристора очень велико). В первом квадранте ток велик, падение напряжения мало — тиристор в данный момент открыт.
Момент перехода из закрытого — в открытое состояние наступает тогда, когда на управляющий электрод подан определенный ток. Переключение из открытого состояния — в закрытое происходит при снижении тока через тиристор. Таким образом, тиристор — это управляемый нелинейный трехполюсник (как и транзистор, у которого ток коллектора зависит от тока базы).
1.5.1. Общие сведения
Нелинейная электрическая цепь это электрическая цепь, содержащая один или несколько нелинейных элементов [ 1 ] .
Нелинейный элемент это элемент электрической цепи, параметры которого зависят от определяющих их величин (сопротивление резистивного элемента от тока и напряжения, ёмкость емкостного элемента от заряда и напряжения, индуктивность индуктивного элемента от магнитного потока и электрического тока).
Таким образом, вольт–амперная u ( i ) характеристика резистивного элемента, вебер–амперная ψ( i ) характеристика индуктивного элемента и кулон–вольтная q ( u ) характеристика емкостного элемента имеют вид не прямой линии (как в случае линейного элемента), а некой кривой, обычно определяемой экспериментально и не имеющей точного аналитического представления.
Нелинейная электрическая цепь обладает рядом существенных отличий от линейной и в ней могут возникать специфические явления
1.5. Нелинейные электрические цепи
Рис. 1.28. УГО нелинейных резистивного, индуктивного и емкостного элементов
(например гистерезис), поэтому этого методы расчёта линейных цепей к нелинейным цепям неприменимы. Особо следует отметить неприменимость к нелинейным цепям метода наложения (суперпозиции).
Важно понимать, что характеристики реальных элементов никогда не бывают линейными, однако в большинстве инженерных расчётов они, с допустимой точностью, могут считаться линейными.
Все полупроводниковые элементы (диоды, транзисторы, тиристоры и т. д.) являются нелинейными элементами.
Условные графические обозначения нелинейных резистивного, индуктивного и емкостного элементов приведены на рис. 1.28 . На выносной площадке мажет указываться параметр, вызывающий нелинейность (например температура для терморезистора)
1.5.2. Параметры нелинейных элементов
Нелинейные элементы характеризуются статическими ( R ст , L ст , и C ст ) и дифференциальными ( R д , L д , и C д ) параметрами.
Статические параметры нелинейного элемента определяются как отношение ординаты выбранной точки характеристики к её абсциссе (рис. 1.29 ).
Статические параметры пропорциональны тангенсу угла наклона прямой, проведённой через начало координат и точку, для которой производится расчёт. Для примера на рис. 1.29 получим:
F ст = y A = m y tg α, x A m x
где α–– угол наклона прямой, проведённой через начало координат и рабочую точку A ;
m y и m x –– масштабы по осям ординат и абсцисс соответственно.
1. Основные положения
Рис. 1.29. К определению статических и дифференциальных параметров
F ст = y A , F диф = dy x A dx
Отсюда статические параметры резистивного, индуктивного и емкостного элементов будут иметь следующий вид:
Дифференциальные параметры нелинейного элемента определяются как отношение малого приращения ординаты выбранной точки характеристики к малому приращению её абсциссы (рис. 1.29 ).
Дифференциальные параметры пропорциональны тангенсу угла наклона касательной в рабочей точке характеристики и осью абсцисс. Для примера на рис. 1.29 получим:
F диф = dy = m y tg β, dx m x
где β –– угол наклона касательной в рабочей точке B характеристики и осью абсцисс;
m y и m x –– масштабы по осям ординат и абсцисс соответственно. Отсюда дифференциальные параметры резистивного, индуктив-
ного и емкостного элементов будут иметь следующий вид:
1.5. Нелинейные электрические цепи
1.5.3. Методы расчёта нелинейных цепей
Нелинейность параметров элементов усложняет расчёт цепи, поэтому в качестве рабочего участка стараются выбрать либо линейный, либо близкий к нему участок характеристики и рассматривают, с допустимой точностью, элемент как линейный. Если же это невозможно или нелинейность характеристики является причиной выбора элемента (особенно это характерно для полупроводниковых элементов), то применяют специальные методы расчёта –– графический , аппроксимации
( аналитической и кусочно–линейной ) и ряд других. Рассмотрим эти методы более подробно.
Идея метода состоит в построении характеристик элементов цепи (вольт–амперной u ( i ), вебер–амперной ψ( i ) или кулон–вольтной q ( u )), а затем, путём их графических преобразований (напр. сложения), получения соответствующей характеристики для всей цепи или её участка.
Графический метод расчёта является наиболее простым и наглядным в применении, обеспечивая в основной массе расчётов необходимую точность, однако он применим для небольшого количества нелинейных элементов в цепи и требует аккуратности при проведении графических построений.
Пример расчёта нелинейной цепи графическим методом для последовательного соединения линейного и нелинейного резистивных элементов приведён на рис. 1.30 , а , для параллельного –– на рис. 1.30 , б .
При расчёте последовательной цепи в одних осях строятся характеристики всех рассчитываемых элементов (для рассматриваемого примера это u нэ ( i ) для нелинейного резистора R нэ и u лэ ( i ) для линейного R лэ ). Характер изменения общего напряжения в цепи u ( i ) определяется путём сложения характеристик нелинейного u нэ ( i ) и линейного u лэ ( i ) элементов u ( i ) = u нэ ( i ) + u лэ ( i ). Сложение производится при одинаковых значении тока (для i = i 0 : u 0 = u нэ 0 + u лэ 0 , см. рис. 1.30 , а .).
Расчёт параллельной цепи производится аналогично, только характеристика всей цепи строится путём сложения токов, при постоянном напряжении (для u = u 0 : i 0 = i нэ 0 + i лэ 0 , см. рис. 1.30 , б .).
