Содержание
История комплексных чисел. Особенности решения многих задач физики и техники при помощи комплексных чисел. Достоинство комплексного метода. Алгебраическая и тригонометрическая форма комплексного импеданса. Механические приложения комплексных чисел.
| Рубрика | Математика |
| Вид | статья |
| Язык | русский |
| Дата добавления | 03.09.2011 |
| Размер файла | 84,6 K |

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Размещено на http://www.allbest.ru/
Применение комплексных чисел в физике
комплексное число физика
1. Комплексное число
Коммплемксные числа — расширение множества вещественных чисел, обычно обозначается С. Любое комплексное число может быть представлено как x + iy, где x и y — действительные числа, i — мнимая единица, то есть число, удовлетворяющее уравнению i 2 = ? 1.
Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени n с комплексными коэффициентами имеет ровно n комплексных корней, то есть верна основная теорема алгебры. Это одна из основных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.
История комплексных чисел
Впервые, по-видимому, мнимые величины появились в известном труде «Великое искусство, или об алгебраических правилах» Кардано (1545), который счёл их непригодными к употреблению. Пользу мнимых величин, в частности, при решении кубического уравнения, в так называемом неприводимом случае (когда вещественные корни многочлена выражаются через кубические корни из мнимых величин), впервые оценил Бомбелли (1572). Он же дал некоторые простейшие правила действий с комплексными числами.
Выражения вида , появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI—XVII веках, однако даже для многих крупных ученых XVII века алгебраическая и геометрическая сущность мнимых величин представлялась неясной. Долгое время было неясно, все ли операции над комплексными числами приводят к комплексным результатам, или, например, извлечение корня может привести к открытию какого-то нового типа чисел. Задача о выражении корней степени n из данного числа была решена в работах Муавра (1707) и Котса (1722).
Символ предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова лат. imaginarius. Он же распространил все стандартные функции, включая логарифм, на комплексную область. Эйлер также высказал в 1751 году мысль об алгебраической замкнутости поля комплексных чисел. К такому же выводу пришел Д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году.
Геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе Весселя (1799). Первые шаги в этом направлении были сделаны Валлисом (Англия) в 1685 году. Арифметическая модель комплексных чисел как пар вещественных чисел была построена Гамильтоном (1837); это доказало непротиворечивость их свойств. Гамильтон предложил и обобщение комплексных чисел — кватернионы, алгебра которых некоммутативна.
2. Комплексные числа в физике
Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами. Комплексные числа широко использовал Н. Е. Жуковский (1847 — 1921) при разработке теории крыла, автором которой он является. Комплексные числа нашли применение во многих вопросах науки и техники.
2.1 Гармонический сигнал
Гармонический сигнал — это гармонические колебания с течением времени распространяющиеся в пространстве, которые несут в себе информацию или какие-то данные и описываются уравнением:
где А — амплитуда сигнала;
— фаза гармонического сигнала;
— циклическая частота сигнала;
Тем не менее, часто используют комплексную запись сигнала:
2.2 Достоинство комплексного метода
Достоинство комплексного метода: при его применении в анализе цепей переменного тока можно применять все известные методы анализа постоянного тока.
Переменный ток — в широком смысле электрический ток, изменяющийся во времени. Мгновенное значение силы i переменного тока меняется во времени по синусоидальному закону: i = Im sin (щt + б), где Im — амплитуда тока, щ = 2рf — его угловая частота, б — начальная фаза. Синусоидальный (гармонический) ток создаётся синусоидальным напряжением той же частоты: u = Um sin (щt + в), где Um — амплитуда напряжения, в — начальная фаза
2.3 Закон Ома
Закон Ома формулируется так: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна характеристике участка, которую называют электрическим сопротивлением этого участка.
Под законом Ома в комплексной форме понимают:
Сопротивление в цепи переменного тока характеризуется не только величиной активного сопротивления r (то, что подразумевается под сопротивлением, когда говорится о цепях постоянного тока), но и индуктивностью L и электрической емкостью С.
Индуктивность — физическая величина, характеризующая магнитные свойства электрической цепи.
Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд.
Комплексное сопротивление участка цепи представляет собой комплексное число, вещественная часть которого соответствует величине активного сопротивления, а коэффициент при мнимой части — реактивному сопротивлению.
Активное сопротивление — сопротивление электрической цепи или её участка, обусловленное необратимыми превращениями электрической энергии в другие виды энергии (в тепловую энергию). Реактивное сопротивление — это сопротивление обусловленное передачей энергии электрическому или магнитному полю (и обратно), с учётом поверхностного эффекта (эффект затухания электромагнитных волн по мере их проникновения в глубь проводящей среды). В результате этого эффекта, например, переменный ток высокой частоты, при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое.
где Z — импеданс, R — величина активного сопротивления, X — величина реактивного сопротивления, i — мнимая единица.
Импедансом называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник. При этом импеданс не должен зависеть от времени.
· j — мнимая единица;
· щ — циклическая частота;
· U(щ), I(щ) — амплитуды напряжения и тока гармонического сигнала на частоте щ;
· цu(щ), цi(щ) — фазы напряжения и тока гармонического сигнала на частоте щ;
· , — Комплексные амплитуды напряжения и тока гармонического сигнала на частоте щ;
Исторически сложилось, что обозначение импеданса, комплексных амплитуд и других комплекснозначных функций частоты записывают как f(jщ), а не f(щ). Такое обозначение показывает, что мы имеем дело с комплексными представлениями гармонических функций вида e j щ t . Кроме того, над символом, обозначающим комплексный сигнал или комплексный импеданс, обычно ставят «домик» или точку: чтобы отличать от соответствующих действительных (некомплексных) величин.
Алгебраическая форма
Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.
Тригонометрическая форма
Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько ток отстаёт от напряжения.
Фаза колебаний — аргумент периодической функции или описывающей гармонический колебательный процесс (щ — угловая частота, t— время, — начальная фаза колебаний, то есть фаза колебаний в начальный момент времени t = 0). Фаза обычно выражается в угловых единицах (радианах, градусах) или в циклах (долях периода): 1 цикл = 2р радиан = 360°. Сдвиг фаз — разность начальных фаз переменных величин, изменяющихся по синусоидальному закону с одинаковой частотой. Сдвиг фаз измеряется в градусах, радианах или долях периода. В электротехнике большое практическое значение имеет сдвиг фаз между напряжением и током, определяющий коэффициент мощности в цепях переменного тока.
2.4 Механические приложения комплексных чисел
Комплексные числа также используются в описании процессов плоского течения жидкости, обтекания профилей жидкостью, волновые движения жидкости. Но поскольку эти процессы не явны для понимания, их рассмотрение на данном этапе считаю нецелесообразным.
комплексное число физика
Комплексные числа широко используются в различных областях физики, в особенности в описании волновых и электромагнитных процессов. С помощью комплексных чисел можно рассчитать параметры для сетей не только постоянного, но и переменного тока.
Список используемой литературы
1. Большая Советская Энциклопедия
2. Яглом И.М. Комплексные числа и их применение в геометрии, М. Физматгиз, 1963
3. Андронов И.К. Математика действительных и комплексных чисел, М. Просвещение, 1975
4. Алешков Ю.З., Смышляев П.П. Теория функций комплексного переменного и ее приложения, изд-во ЛГУ, 1986
5. Роджерс Э. Физика для любознательных, М., 1971
Размещено на Allbest
Подобные документы
История комплексных чисел. Соглашение о комплексных числах. Геометрический смысл сложения и вычитания комплексных чисел. Геометрическая интерпретация комплексных чисел. Длина отрезка. Уравнение высших степеней, уравнение деления круга на пять частей.
реферат [325,7 K], добавлен 25.10.2012
Появление отрицательных чисел. Понятие мнимых и комплексных чисел. Формула Эйлера, связывающая показательную функцию с тригонометрической. Изображение комплексного числа на координатной плоскости. "Гиперкомплексные" числа Гамильтона ("кватернионы").
презентация [435,9 K], добавлен 16.12.2011
Комплексные числа в алгебраической форме. Степень мнимой единицы. Геометрическая интерпретация комплексных чисел. Тригонометрическая форма. Приложение теории комплексных чисел к решению уравнений 3-й и 4-й степени. Комплексные числа и параметры.
дипломная работа [1,1 M], добавлен 10.12.2008
Система, свойства и модели комплексных чисел. Категоричность и непротиворечивость аксиоматической теории комплексных чисел. Корень четной степени из отрицательного числа. Матрицы второго порядка, действительные числа. Операции сложения и умножения матриц.
курсовая работа [1,1 M], добавлен 15.06.2011
Об истории возникновения комплексных чисел и их роли в процессе развития математики. Алгебраические действия над комплексными числами и их геометрический смысл. Применение комплексных чисел к решению алгебраических уравнений 3-ей и 4-ой степеней.
курсовая работа [104,1 K], добавлен 03.01.2008
Понятие комплексных чисел, стандартная, матричная и геометрическая модели; действия над комплексными числами; модуль и аргумент. Алгебраическое, тригонометрическое и показательное представление комплексных чисел. Формула Муавра и извлечение корней.
контрольная работа [25,7 K], добавлен 29.05.2012
Расчет значений комплексных чисел в алгебраической, тригонометрической и показательной формах. Определение расстояния между точками на комплексной плоскости. Решение уравнения на множестве комплексных чисел. Методы Крамера, обратной матрицы и Гаусса.
контрольная работа [152,7 K], добавлен 12.11.2012
Геометрическое представление комплексных чисел, алгебраическая и тригонометрическая формы. Свойства арифметических операций над комплексными числами: правила сложения (вычитания) их радиус-векторов, произведение (частное) модуля числа; формула Муавра.
презентация [147,4 K], добавлен 17.09.2013
Вычисление комплексных чисел, модуля и аргумента, извлечение кубических корней. Нахождение синусов и косинусов в алгебраическом виде. Решение системы уравнений с помощью формул Крамера, вспомогательных определителей и средствами матричного исчисления.
контрольная работа [444,2 K], добавлен 11.05.2013
Мнимые и действительные, равные и сопряжённые комплексные числа; модуль и аргумент. Арифметические действия над множеством комплексных чисел: сумма, разность, произведение, деление. Представление комплексных чисел на координатной комплексной плоскости.
презентация [60,3 K], добавлен 17.09.2013
Комплексные числа в физике
По мере дальнейшего путешествия в миры шаманизма, психологии и физики мы будем снова исследовать комплексные числа. А пока давайте на несколько минут расслабимся и перенесемся в своей фантазии вперед во времени через сотни лет, от открытия комплексных чисел в XV в. до квантовой физики XX века.
Конъюгация служит ключом не только к психологии сознания, но и к физике наблюдения. В физике такие материальные объекты, как электроны, описываются тем, что именуется волновыми функциями, которые представляют собой просто комплексные числа. Волновая функция описывает паттерны поведения электрона – то, как ведет себя электрон в тех или иных обстоятельствах.
Мы уже видели, что такой объект, как береза, имеет и реальные, и воображаемые аспекты – это дерево «береза», а также «заботливое» дерево. Таким образом, мы обнаружили, что любое наблюдение носит отчасти реальный и отчасти воображаемый характер. По аналогии электроны, которые можно описывать комплексными числами, тоже являются отчасти реальными и отчасти воображаемыми. Мы не можем знать об электроне все. Некоторые из его характеристик остаются неопределенными. Физики не могут измерять все поведение электрона, поскольку не могут измерять комплексные числа.
У физиков есть основная формула – волновая функция, комплексные числа, которые описывают материю. Для описания материи физикам необходимы эти частично воображаемые комплексные числа. Но здесь возникает проблема! Измеримую реальность материи нельзя описывать мнимыми числами. Числа, описывающие реальность, должны быть действительными, а мнимые числа не обладают реальностью в повседневной жизни. Поэтому физики решили использовать особое свойство комплексных чисел – при конъюгации комплексные числа становятся действительными. Конъюгация комплексных чисел устраняет мнимые аспекты, не поддающиеся измерению.
Если одно число волновой функции, скажем 3 – 4i, подвергается конъюгации, то результат (25) не содержит мнимых чисел. Это действительное число скрывает мнимое. Оно больше не показывает корни 25. Оно скрывает тот факт, что оно было получено в результате умножения (3 – 4i) х (3 + 4i). В известном смысле можно сказать, что действительные числа скрывают свою подоплеку – комплексные числа и процесс отражения. По аналогии мы также могли бы сказать, что реальность имеет скрытую подоплеку сновидения!
Физики могут проверять и измерять продукт конъюгации, то есть действительное число вроде 25. В какой-то момент физики решили не беспокоиться о смысле процесса отражения, необходимого для получения действительных чисел, а именно (3 – 4i) х (3 + 4i). В конце концов, они же не знали, к чему в повседневной, общепринятой реальности относятся такие комплексные числа, как 3 + 4i. Комплексные числа и процесс конъюгации, дающий начало действительным результатам, так и не были поняты. Теперь у нас есть метафора для осмысления их значимости.
Комплексные числа имеют аналоги в сфере чувственного восприятия НОР. Более того, их конъюгация создает действительные числа посредством процесса осознанности и отражения. Знание этого дает нам намек на значение того, что происходит в квантовой физике.
Мы увидим, что электроны и их волновые функции подобны сновидениям в том смысле, что при отражении или усилении, то есть конъюгации, они развертываются в реальность измерений субатомных частиц. Это усиление аналогично тому, как конъюгация развертывает сновидения в повседневную жизнь.
Иными словами, и в психологии, и в физике основу понимания реальности составляют чувственные переживания. Чувственный опыт лежит в основе процесса наблюдения. Он дает нам намеки в отношении сущности материи – Вселенной, в которой все мы живем и дышим, – и ключей к ее пониманию.
До сих пор физика использовала математику как инструмент, и не сосредоточивалась на смысле своей математики. Поэтому физики непреднамеренно игнорировали чувственный опыт. Большинство из нас подобны физикам. И вы, и я постоянно подавляем наши комплексные числа, призрачные фантазии, наши чувственные переживания и процессы отражения. Нам либо не с кем их обсуждать, либо мы их забываем, если они кажутся нам вздором. Мы нередко стараемся обходить сферу воображения и сосредоточивать все свои переживания на общепринятой реальности.
Мы ищем только наиболее вероятный смысл чего-либо, его действительное числовое значение. Метафорически говоря, глядя только на действительное значение опыта, мы получаем ответы в реальности, но игнорируем чувственный опыт, подобный сновидению, и процесс отражения, скрытые за реальностью. Как мы видели в начале нашего путешествия, общепринятая реальность подобна дереву, корни которого уходят в необщепринятую, или чувственную, сферу.
Например, допустим, вы рассказываете мне, что видели сон о дереве. Если я спрошу вас: «Что это означает в общепринятой реальности?» – вам придется дать мне его наиболее вероятное действительное значение. Мой вопрос о дереве маргинализирует опыт отражения и конъюгации. Вместо этого, я мог бы попросить вас осознанно развертывать то сновидение, снова представляя его себе и прослеживая его развертывание в виде образов и других переживаний.
Развертывание отличается от расспрашивания или интерпретирования. Развертывание посредством осознанного сновидения отдает должное иррациональному – переживаниям, которые порождают сознание. Опыт развертывания или конъюгации дает нам ощущение того, что в основе всей реальности лежит сновидение. Вопрос только в том, что «означает» сновидение, обращается только к его ОР-атрибутам и игнорирует его удивительные корни. По контрасту, конъюгация, или осознанное сновидение, сосредоточивается на НОР-опыте бытия деревом. Такие переживания – самое близкое, насколько мы можем подойти к основам реальности.
Понятно, что физика сосредоточивается главным образом на ОР и действительных числах. В конце концов, физика определяет себя как изучение общепринятых восприятий. Но наука забыла, что ее определение носит самоограничивающий характер и маргинализирует психологический опыт. Физика избегает изучения необщепринятых аспектов наблюдения, вроде личности наблюдателя или чувств, которые вызывает объект наблюдения. Физика теряет связь со своей математикой, своими комплексными числами, своими волновыми функциями и призрачной реальностью позади ОР. Однако изучение призрачных сфер не утеряно: там, где заканчивается современная физика, начинаются традиционный шаманизм и психология.
Мы увидели, что закономерности, обнаруживающиеся в психологии восприятия и в шаманском опыте, согласуются с принципами математики и, как мы теперь знаем, физики. Это соответствие указывает на единое поле – подобную сновидению субстанцию опыта, которая лежит в основе жизни, в основе психологии и физики, электронов и их наблюдателей, всех нас. Это поле – основа развертывания 1, 2, 3 и бесконечности.
В дальнейшем мы более подробно узнаем о том, как осознанное сновидение кодируется внутри. То же осознанное сновидение, что порождает сознание и реальность в психологии, дает нам основу для понимания невидимой сферы квантовых объектов и мира, в котором мы живем, – основную субстанцию Вселенной.
В современной математике комплексное число является одним из фундаментальнейших понятий, находящее применение и в «чистой науке», и в прикладных областях. Понятно, что так было далеко не всегда. В далекие времена, когда даже обычные отрицательные числа казались странным и сомнительным нововведением, необходимость расширения на них операции извлечения квадратного корня была вовсе неочевидной. Тем не менее, в середине XVI века математик Рафаэль Бомбелли вводит комплексные (в данном случае точнее сказать, мнимые) числа в оборот. Собственно, предлагаю посмотреть, в чем была суть затруднений, доведших в итоге солидного итальянца до подобных крайностей.
Существует распространенное заблуждение, что комплексные числа потребовались для того, чтобы решать квадратные уравнения. На самом деле, это совершенно не так: задача поиска корней квадратного уравнения никоим образом введение комплексных чисел не мотивирует. Вот совершенно.
Давайте убедимся сами. Всякое квадратное уравнение можно представить в виде:
 .
.
Геометрически, это означает, что мы хотим найти точки пресечения некоторой прямой  и параболы
и параболы 
Я тут даже картинку сделал, для иллюстрации.

Как нам всем хорошо известно из школы, корни квадратного уравнения (в указанных выше обозначениях) находятся по следующей формуле:

Оказываются возможными 3 варианта:
1. Подкоренное выражение положительно.
2. Подкоренное выражение равно нулю.
3. Подкоренное выражение отрицательно.
В первом случае имеются 2 различных корня, во втором два совпадающих, в третьем уравнение «не решается». Все эти случаи имеют вполне наглядную геометрическую интерпретацию:
1. Прямая пересекает параболу (синяя прямая на рисунке).
2. Прямая касается параболы.
3. Прямая не имеет с параболой общих точек (сиреневая прямая на рисунке).
Ситуация проста, логична, непротиворечива. Пытаться извлекать квадратный корень из отрицательного числа нет совершенно никаких оснований. Никто и не пытался.
Обстановка существенно изменилась, когда пытливая математическая мысль добралась до кубических уравнений. Чуть менее очевидно, используя некоторую несложную подстановку, всякое кубическое уравнение можно свести к виду:  . С геометрической точки зрения ситуация похожа на предыдущую: мы ищем точку пересечения прямой и кубической параболы.
. С геометрической точки зрения ситуация похожа на предыдущую: мы ищем точку пересечения прямой и кубической параболы.
Взгляните на картинку:

Существенное отличие от случая квадратного уравнения в том, что какую бы прямую мы не взяли, она всегда пересечет параболу. Т.е., уже из чисто геометрических соображений, кубическое уравнение всегда имеет хотя бы одно решение.
Найти его можно воспользовавшись формулой Кардано:

где
 .
.
Немного громоздко, но пока, вроде бы, все в порядке. Или нет?
Вообще, формула Кардано — это яркий пример «принципа Арнольда» в действии. И что характерно, Кардано никогда на авторство формулы не претендовал.
Вернемся, однако, к нашим баранам. Формула замечательная, без преувеличение великое достижение математики начала-середины XVI века. Но есть у нее один нюанс.
Возьмем классический пример, который рассматривал еще Бомбелли:
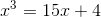 .
.
Внезапно,
 ,
,
и, соответственно,
 .
.
Приплыли. А формулу жалко, а формула-то хорошая. Тупик. При том, что решение у уравнения, безусловно, есть.
Идея Рафаэля Бомбелли заключалась в следующем: давайте прикинемся шлангом и сделаем вид, что корень из отрицательного — это какое-то число. Мы, конечно, знаем, что таких чисел нет, но тем не менее, давайте представим, что оно существует и его, как обычные числа, можно складывать с другими, умножать, возводить в степень и т.п.
Используя подобный подход, Бомбелли установил, в частности, что
 ,
,
и
 .
.
Давайте проверим:
 .
.
Заметьте, в выкладках никаких предположений о свойствах квадратных корней из отрицательных чисел не предполагалось, кроме упомянутого выше допущения, что они ведут себя как «обычные» числа.
В сумме получаем  . Что вполне себе правильный ответ, который элементарно проверяется прямой подстановкой. Это был настоящий прорыв. Прорыв в комплексную плоскость.
. Что вполне себе правильный ответ, который элементарно проверяется прямой подстановкой. Это был настоящий прорыв. Прорыв в комплексную плоскость.
Тем не менее, подобные выкладки выглядят как некоторая магия, математический фокус. Отношение к ним, как к некоему трюку, сохранялось среди математиков еще очень долго. Собственно, придуманное Рене Декартом для корней из отрицательных название «мнимые числа» вполне отражает отношение математиков тех времен к таким развлечениям.
Однако, время шло, «трюк» применялся с неизменным успехом, авторитет «мнимых чисел» в глазах математического общества рос, сдерживаемый, однако, неудобством их использования. Лишь получение Леонардом Эйлером (кстати, это именно он ввел ныне общеупотребительное обозначение  для мнимой единицы) знаменитой формулы
для мнимой единицы) знаменитой формулы

открыло комплексным числам дорогу в самые различные области математики и ее приложений. Но это уже совсем другая история.
 .
. Геометрически, это означает, что мы хотим найти точки пресечения некоторой прямой
 и параболы
и параболы 
Я тут даже картинку сделал, для иллюстрации.

Как нам всем хорошо известно из школы, корни квадратного уравнения (в указанных выше обозначениях) находятся по следующей формуле:

1. Подкоренное выражение положительно.
2. Подкоренное выражение равно нулю.
3. Подкоренное выражение отрицательно.
1. Прямая пересекает параболу (синяя прямая на рисунке).
2. Прямая касается параболы.
3. Прямая не имеет с параболой общих точек (сиреневая прямая на рисунке).
 . С геометрической точки зрения ситуация похожа на предыдущую: мы ищем точку пересечения прямой и кубической параболы.
. С геометрической точки зрения ситуация похожа на предыдущую: мы ищем точку пересечения прямой и кубической параболы. Взгляните на картинку:

Найти его можно воспользовавшись формулой Кардано:

где
 .
. Немного громоздко, но пока, вроде бы, все в порядке. Или нет?
Возьмем классический пример, который рассматривал еще Бомбелли:
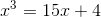 .
. Внезапно,
 ,
, и, соответственно,
 .
. Приплыли. А формулу жалко, а формула-то хорошая. Тупик. При том, что решение у уравнения, безусловно, есть.
 ,
, и
 .
. Давайте проверим:
 .
. Заметьте, в выкладках никаких предположений о свойствах квадратных корней из отрицательных чисел не предполагалось, кроме упомянутого выше допущения, что они ведут себя как «обычные» числа.
 . Что вполне себе правильный ответ, который элементарно проверяется прямой подстановкой. Это был настоящий прорыв. Прорыв в комплексную плоскость.
. Что вполне себе правильный ответ, который элементарно проверяется прямой подстановкой. Это был настоящий прорыв. Прорыв в комплексную плоскость. для мнимой единицы) знаменитой формулы
для мнимой единицы) знаменитой формулы 
открыло комплексным числам дорогу в самые различные области математики и ее приложений. Но это уже совсем другая история.






