Содержание
Даже беглый взгляд на галерею многогранников доказывает, что звёздчатые многогранники являются очень красивыми и декоративными. Совсем не сложно своими руками изготовить модель понравившегося многогранника из бумаги или картона. Всё, что требуется для создания бумажной модели — цветной картон, ножницы и клей.
Наиболее фундаментальным русскоязычным руководством по изготовлению бумажных моделей многогранников является книга: Веннинджер "Модели многогранников", 1974
В ней даются подробные инструкции по изготовлению 119-ти бумажных моделей многогранников, в том числе всех 75 однородных многогранников (включая правильные и полуправильные выпуклые и звездчатые многогранники), а также наиболее красивых звездчатых форм икосаэдра, икосододекаэдра и кубооктаэдра. В книге приводятся трафареты и шаблоны для вырезания из бумаги составных частей будущей модели (заготовок), а также даются схемы соединения частей между собой и таблицы раскраски. В тоже время читателю оставлена свобода для творчества: для некоторых моделей Веннинджер предлагает самостоятельно найти способ соединения деталей, дающий требуемую раскраску, или подумать над возможными вариантами раскраски. После прочтения книги Веннинджера вы научитесь самостоятельно проектировать новые звездчатые формы и изготавливать их модели из бумаги.
Изложение материала в книге Веннинджера эволюционное: в начале рассматривается понятие многогранника, описываются простые для понимания и изготовления модели правильных и полуправильных выпуклых многогранников (см. таблицу). Затем вводится понятие звездчатых форм, трехмерный калейдоскоп, анализируются принципы построения звездоформ и рассматриваются соответствующие бумажные модели. Завершается книга математическим определением и изготовлением моделей всех невыпуклых однородных многогранников, в том числе очень сложных "курносых" моделей. По причине эволюционности желательно читать книгу с самого начала, по крайней мере следует прочитать общие указания об изготовлении моделей, замечания о звездчатых формах и соединениях, а при изготовлении более сложных моделей надо читать соответствующие предварительные замечания. Единственный недостаток книги — увы, не цветные фотографии готовых моделей. Впрочем, вы можете смотреть интерактивные трехмерные модели соответствующих многогранников на этом сайте: в следующей таблице перечислены все модели из книги Веннинджер и даны ссылки на трехмерные модели и инструкции Веннинджера по изготовлению моделей многогранников из бумаги (чтобы увидеть примерный внешний вид готовой модели из бумаги, подведите курсор к соответствующей ссылке).
В нашей стране весомый вклад в изготовление и популяризацию бумажных моделей многогранников внесла Гончар Валентина Васильевна, архитектор и руководитель кружка бумажного моделирования. Её книги "Кристаллы" (1994) и "Модели многогранников" (1997, 2010) посвящены в основном платоновым и архимедовым телам, а также их отдельным звездчатым формам. Гончар В.В. предлагает упростить создание бумажных моделей за счет использования не заготовок отдельных граней, а единой выкройки, что сделает моделирование доступным даже для детей. Значительно преуспели в создании единых трафаретов и зарубежные авторы, причем трафареты найдены не только для выпуклых многогранников, но и даже для некоторых невыпуклых многогранников. В таблице ниже для примера даны ссылки на соответствующие трафареты и фотографии бумажных моделей сайта www.korthalsaltes.com. Впрочем, математику соответствующее упрощение раскраски моделей (вплоть до одноцветной) может показаться некоторым недостатком.
Другое направление, развитое Валентиной Васильевной — создание моделей многогранников в технике оригами (в идеале, без использования клея и ножниц). Ею создан "универсальный модуль оригами", складывая который можно получать отдельные звездчатые многогранники, и даже делать оригинальные подвижные модели — трансформеры. Созданная Валентиной модель-трансформер "раскрывающийся цветок" (видео, инструкции по изготовлению) получила всемирное признание.
Вплотную к созданию моделей многогранников из бумаги примыкает искусство кусудамы, т.е. создание красивых цветных шаров из бумаги. Некоторые кусудамы сами являются многогранниками, другие лишь сохраняют хорошо заметную симметрию правильных многогранников. Основная цель кусудам — эстетичный внешний вид бумажных моделей, кусудамы часто украшают бусинками, кисточками и т.д., о математической стрости в раскраске и строении речь не идет (впрочем, несомненна связь групп симметрии многогранников и внешней привлекательности кусудам). Приведенные примеры фотографий кусудами взяты с сайта http://ru-kusudama.livejournal.com.
В 2011 году издательство "Многогранники" поставило изготовление многогранников из бумаги на надежные коммерческие рельсы. Оно выпускает наборы "Волшебные грани". Каждый набор посвящен конкретному многограннику и содержит вырезанные и подогнанные детали, а также инструкции по изготовлению. Следует отметить отлично оформленный сайт, содержащий фотографии готовых моделей, видеоинструкции по их изготовлению (конечно, только из соответствующих наборов) и другие материалы. К сожалению, пока номенклатура многогранников из наборов "Волшебные грани" весьма ограничена; в таблице ниже представлен список ссылок на многогранники, для которых издавались наборы "Волшебные грани".
О сложности изготовления бумажных моделей многогранников
В столбце "Сложность" таблицы указано число деталей (граней), из которых состоит многогранник, а также количество различных типов шаблонов, которые потребуются для изготовления этих деталей из бумаги. Конечно, такое количество деталей потребуется, только если при изготовлении бумажной модели многогранника смежные грани раскрашиваются в различные цвета. Для однородных многогранников это оптимальный способ раскраски, но для звёздчатых форм и особенно соединений тел другая раскраска может оказаться более правильной и интересной. И всякий раз, когда смежные грани окрашиваются в одинаковый цвет, можно упростить изготовление модели, уменьшив количество заготовок и клеевых соединений. Например, модель "соединение пяти тетраэдров" имеет 60 граней (рисунок слева), но если каждый тетраэдр раскрашивать в свой цвет, то модель можно будет собрать всего из 20 деталей, по 4 детали каждого цвета (рисунок справа). В самом простом случае каждый выпуклый многогранник (а также некоторые не выпуклые) может быть изготовлен из единственной заготовки, однако при этом (если не использовать цветной принтер) получится лишь одноцветная модель. Впрочем, зачастую упрощенно раскрашенные или даже одноцветные бумажные модели многогранников весьма эффектны.
Представляю Вам новую свою схему и видеоинструкцию по сборке одного из тел Кеплера-Пуансо* — малого звёздчатого додекаэдра.
Малый звёздчатый додекаэдр является одним из четырёх невыпуклых правильных многогранников. Он состоит из 12 граней в виде пентаграмм с пятью пентаграммами, сходящимися в каждой вершине. Он имеет то же самое расположение вершин, что и выпуклый правильный икосаэдр. Кроме того, у него то же самое расположение рёбер, что и у большого икосаэдра. Этот многогранник считается первой звёздчатой формой додекаэдра.
*Тело Кеплера-Пуансо — это тело, представляющее собой правильный звёздчатый многогранник, не являющийся соединением платоновых и звёздчатых тел.
Для развёртки малого звёздчатого додекаэдра необходимо 6 листов цветного картона формата А4. Длина ребра получается 8 см, а высота многогранника — около 25 см. Ссылка на развёртку в формате pdf или картинками ниже:
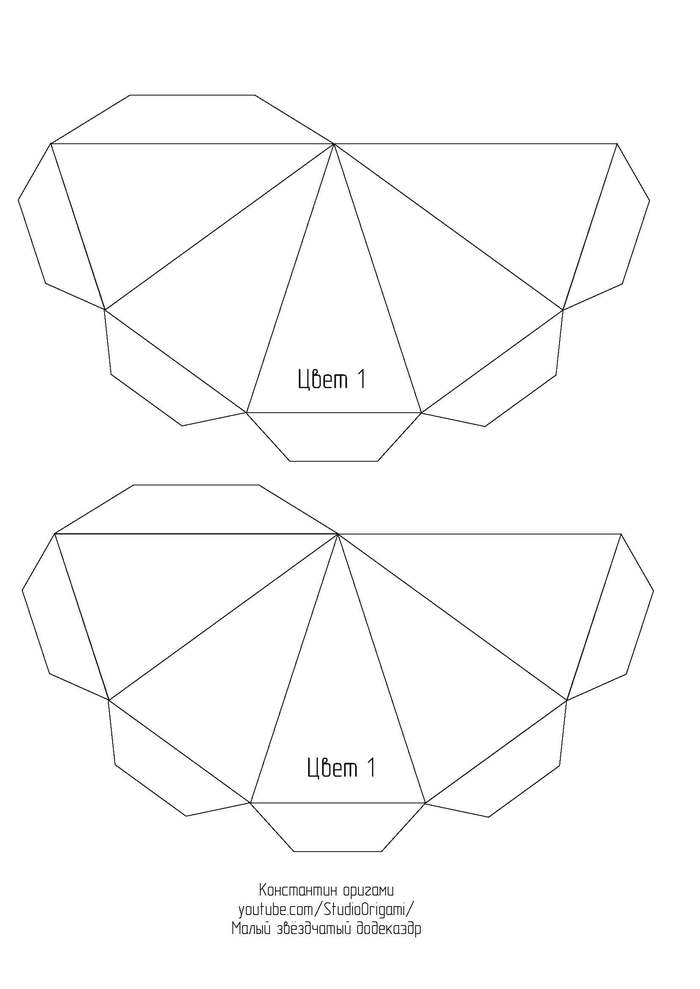
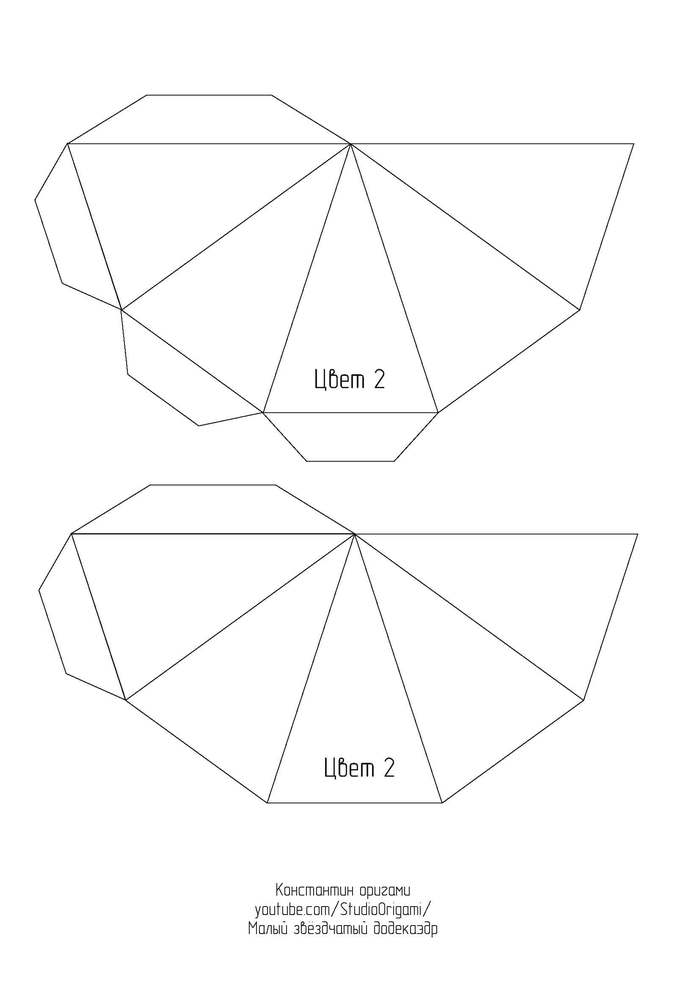
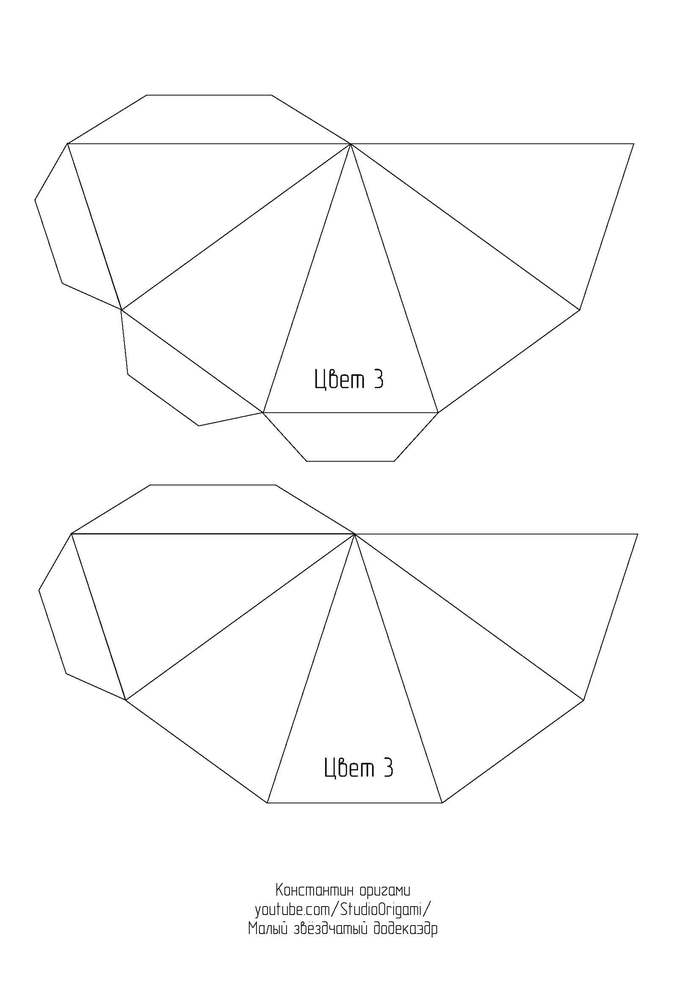
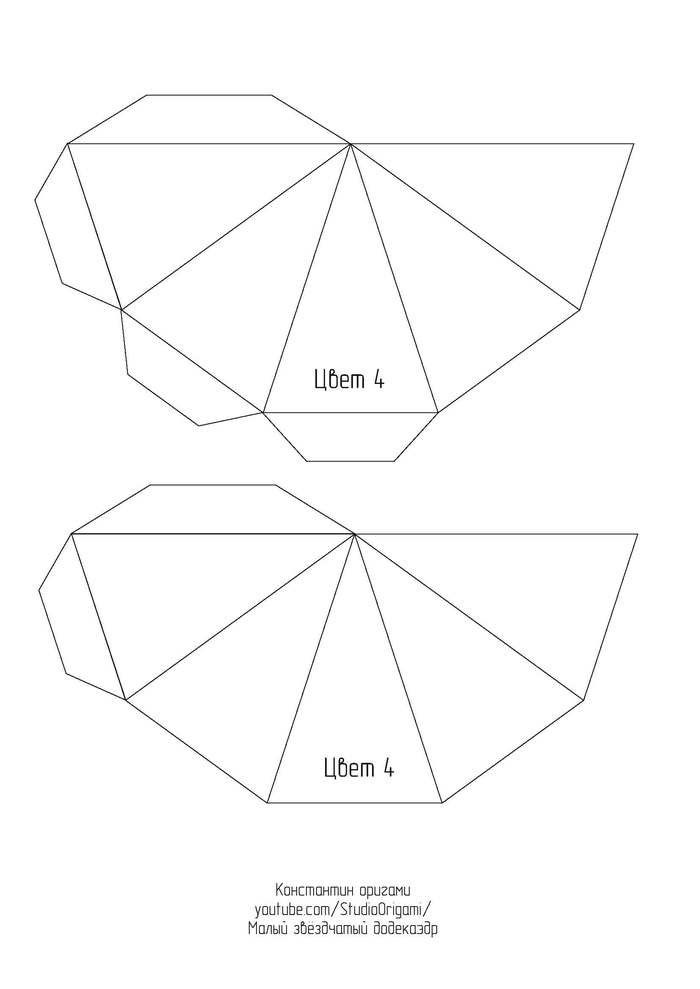
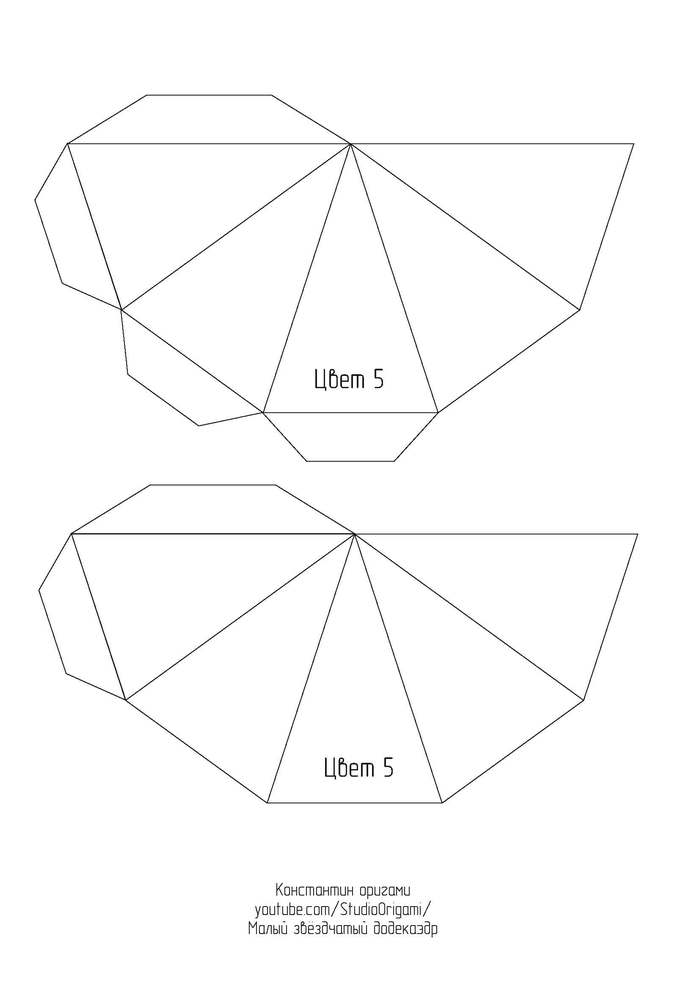
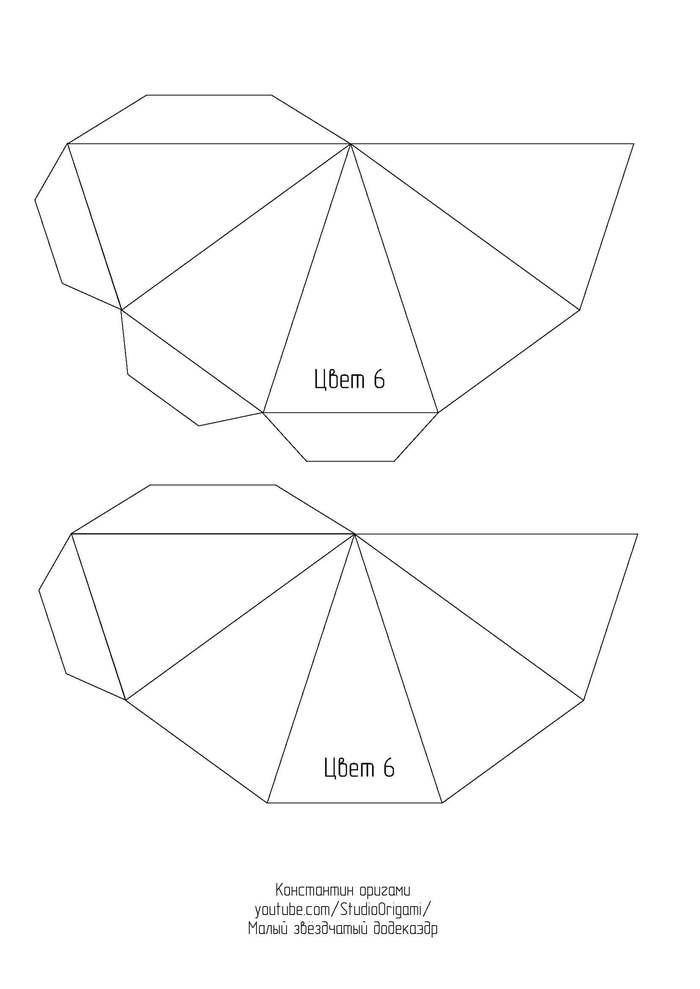
Также смотрите видеоинструкцию по сборке многогранника:
Если понравилось, то смотрите предыдущие мои посты про многогранники:
Найдены возможные дубликаты
было дело =) соединение пяти тетраэдров
Ностальгия. Школа. Стереометрия.
Повезло Вам, у нас такого в школе ничего не было.
Мы в университете клеили завершающую форму звездчатого икосаэдра. Где-то даже фотографии в архиве были
О сообществе
Умеешь делать что-то своими руками? Поделись этим умением со всеми!
Вопросы и ответы найдете вот тут -> FAQ
Общий чат Telegram
Прежде чем постить в сообществе, прочтите руководство.
1. Общение строится на взаимном уважении и доверии.
2. Старайтесь не делать грамматических ошибок в сообщениях – это создаст негативное впечатление о вас. Грамотность – залог комфортного пребывания в Сообществе.
3. Фотографии, загружаемые в Сообщество, должны быть четкими, не замыленными, с достаточным светом.
4. Вы можете размещать ссылки на страницы в социальных сетях ТОЛЬКО в конце поста. Только ссылку. С условиями, что ни в посте, ни далее по ссылке не будет рекламных предложений(В посте, в комментариях и по ссылке не должно быть продаж, указания цен и коммерческих предложений) 4.1. В комментариях контакты запрещены
5. Ставьте тег "рукоделие с процессом", если у вас показан процесс создания изделия, и наоборот, "рукоделие без процесса", если процесса нет. Это поможет пользователям, которые ищут инструкцию как сделать изделие
Одной из простейших бумажных кусудам считается додекаэдр-оригами. Но это не значит, что он выглядит неэффектно, особенно когда речь идёт о звёздчатой разновидности. Декоративный многогранник, подобно другим своим родственникам – кусудамам, отлично подходит для праздничного украшения помещений или в качестве оригинального подарка. Мини-додекаэдры можно использовать как модные украшения, сделав из них серьги или кулон.
Ажурная модель
Существует несколько типов оригами-додекаэдров, но сделать эту прозрачную конструкцию из бумажных модулей проще всего. Хорошее задание для детей, желающих познакомиться с азами пространственной геометрии и взрослых, ищущих эффективное средство для снятия стресса. Желательно использовать для игрушки бумагу ками с рисунком, она придаст особый шарм и колорит.
Пошаговая инструкция:
- Для создания кусудамы понадобится 30 одинаковых модулей. Их складывают из прямоугольников, имеющих соотношение сторон 3:4. Например, размером 6х8 см, 9х12 см и так далее. Можно брать как одно-, так и двухсторонние листы.
- Складываем каждый прямоугольник пополам вдоль длинной стороны. После чего делаем Z-образный сгиб.
- Располагаем получившуюся полоску длинной стороной к себе. Загибаем правый нижний угол вверх. Переворачиваем заготовку на 180°. И повторяем действие для правого нижнего угла (другого).
- Складываем фигуру по диагонали, как показано на рис 4.
- Модули для додекаэдра-кусудамы готовы.
Остаётся соединить их в пространственную композицию. Для этого короткую часть одного модуля вставляем к «карман» длинной части другого. И располагаем так, чтобы внутренние углы и грани обоих элементов совпали.
Аналогичный образом добавляем третий модуль, соединяя его с предыдущими двумя и формируя устойчивый конструктивный узел.
Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.
За счёт необычной бумаги с принтом, получается стильный предмет декора. Чтобы кусудама не распадалась, лучше соединить узловые элементы с помощью клея.
Подробная сборка ажурного додекаэдра представлена и в видео-МК:
Кусудама из правильных пятиугольников
Схема сборки додекаэдра-оригами из пентагонов – равносторонних пятиугольников, разработана американским дизайнером Дэвидом Брилом. Для модулей он использует 12 листов формата А6, то есть 10,5х14,8 см.
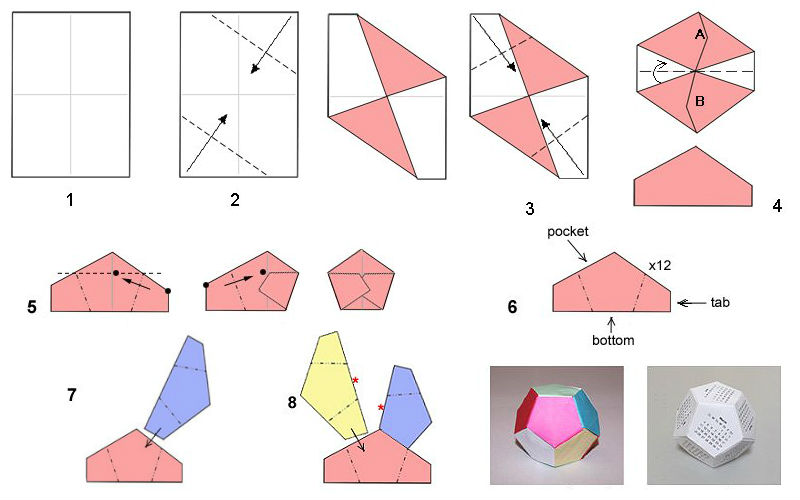
Пошаговая инструкция:
- Исходный прямоугольник складываем пополам в продольном и поперечном направлении, намечая серединные оси.
- Правый верхний и левый нижний угол сгибаем к центру. Получаем своего рода полуконверт.
- Аналогично складываем противоположные углы.
- Пятиугольную заготовку, «закрываем» сверху вниз «долиной».
- Верхний угол опускаем вниз и возвращаем обратно. На месте пересечения получившейся линии с вертикальной осью фигуры, образуется точка. К ней поочерёдно сгибаем внешние углы.
- Модуль-пентагон готов. Последние два сгиба раскрываем – это будут детали крепления элементов между собой.
- Боковые «ушки» одной детали вставляем в «карманы» другой. Места соединения для надёжности фиксируем клеем.
- Продолжаем сборку, пока не используем все 12 модулей.
Из подобных додекаэдров часто делают настольные календари. На каждой грани как раз размещается по месяцу. Соответствующие распечатки с числами и днями недели, можно скачать из интернета и наклеить на стенки модели. Получится не только красиво, но и практично.
Додекаэдр-звезда
Правильные звёздчатые многогранники относятся к самым красивым геометрическим фигурам. С момента своего открытия в XVI веке, они считались символом совершенства Вселенной. Малый звёздчатый додекаэдр впервые построил немецкий астроном и математик Иоганн Кеплер – создатель знаменитой теории о строении Солнечной системы. Многогранник имеет собственное имя: Арур Кэли, в честь английского учёного, сделавшего огромный вклад в развитие линейной алгебры.
Малый звёздчатый додекаэдр-оригами представляет собой фигуру из 12 граней-пентаграмм, с пятью пентаграммами, сходящимися к вершинам. Он состоит из 30 модулей, которые складываются из квадратов, размером 8х8 см. Лучше всего использовать профессиональную бумагу-оригами, которая позволит создавать чёткие грани и жёсткие узлы, не позволяющие конструкции распадаться или деформироваться.
Интересные факты о додекаэдре
Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.
Нечто подобное предполагал и живший в V в. до н. э. древнегреческий философ Платон. В своём учении о классических стихиях, он назвал додекаэдр «образцом божественного устройства Космоса». Вообще же все пять известных правильных многогранников до сих пор называют Платоновыми телами, по имени мыслителя, впервые выстроившего с их помощью чёткую картину мироздания.
Пентагон, лежащий в основе додекаэдра, построен на принципах «золотого сечения». Эта пропорция, которую древние греки считали «божественной» часто встречается в природе. Интересно, что соотношения «золотого сечения» присущи лишь додекаэдру и икосаэдру, у трёх других Платоновых тел его нет.
Игрушки древних римлян
На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины. Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной. Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.
Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.
В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр. Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее. В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.
Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.
